作者简介:孙宗岐(1979—),西京学院副教授.研究方向:随机分析与运筹. E-mail: szqi200679@sina.com
中文责编:方 圆; 英文责编:淡 紫
1)西京学院医学院,陕西西安 710123; 2)西京学院理学院,陕西西安 710123
运筹学; 对策论; 复合Poisson-Geometric过程; 风险投资; 障碍分红; Gerber-Shiu函数; 破产时刻Laplace变换
1)Medical College, Xijing University, Xi'an 710123, Shaanxi Province, P.R.China2)College of Science, Xijing University, Xi'an 710123, Shaanxi Province, P.R.China
operations research; game theory; compound Poisson-Geometric process; venture capital investment; barrier dividend; Gerber-Shiu function; Laplace transform of ruin time
DOI: 10.3724/SP.J.1249.2021.02214
在保险资金的管理中,线性障碍分红和阈值分红是保险公司常考虑到的分红机制,因此,在复合风险下,带投资与线性障碍分红的Gerber-Shiu函数问题也是一个值得研究的问题.GERBER等[1]提出一种分析保险盈余过程精算特征的Gerber-Shiu期望折现惩罚函数(Gerber-Shiu函数),其在刻画保险公司破产时刻的Laplace变换、破产概率、破产时瞬间盈余及破产时的赤字分布时均有统一的微分-积分方程,因此,该函数受到广泛研究关注.LIN等[2]将该函数引入考虑分红的经典风险模型中,研究破产时刻的Laplace变换.赵金娥等[3]利用Gerber-Shiu函数研究障碍分红下赔付到来为P-稀疏过程破产时刻的Laplace变换问题.陈洁等[4]研究离散风险模型中带障碍分红的Gerber-Shiu函数,在指数分布下得到破产时刻的Laplace变换显式解; 韩树新等[5]考虑两类稀疏风险模型中带障碍分红的Gerber-Shiu函数问题,也在指数分布下得到破产时刻的Laplace变换显式解.然而以上研究都没有考虑保险实务中普遍存在的免赔额规定和无赔款保费折扣优待制度.
毛泽春等[6]基于保单免赔规定和无赔款保费折扣优待制度,提出复合Poisson-Geometric过程(复合P-G过程),很好刻画了赔付和索赔不对等的事实,并利用偏离系数精确刻画二者之间的不对等程度.贺丽娟等[7]在复合P-G风险下研究变保费率的Gerber-Shiu函数,乔克林等[8]也在复合P-G风险下继续考虑带风险投资的复合P-G风险破产概率.YANG等[9]得到带扰动的相依风险模型Gerber-Shiu函数所满足的积分方程,最后在指数分布下给出Gerber-Shiu函数所满足的显式解.苏必超等[10]利用概率的计算性质,给出破产时刻的概率密度函数.在复合风险下,孙宗岐等[11-12]研究保险公司的破产概率及带投资的障碍分红问题.然而以上研究没有考虑分红或投资,大多也未能得到破产时刻的Laplace变换显式解.
为了使风险模型更接近保险公司的实际运作情况,基于以上研究现状,本文研究复合风险下,带投资和障碍分红时,保险公司破产时刻的Laplace变换问题,并在指数分布下求解破产时刻的Laplace变换显式解.
假设所有随机过程和随机变量都定义在完备概率空间(Ω,Ft,F,P)上.先给出保费过程、赔付过程、盈余过程及障碍分红的数学模型.
通过分析索赔事件与赔付事件不对等的事实,毛泽春等[6]提出如下复合P-G过程.
定义1 设λ>0, 0≤γ<1, 称非负整值随机变量N服从参数为λ和γ的复合P-G分布,如果其矩母函数为
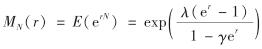
其中, γ为偏离系数; r为任意实数.当γ=0时,MN(r)=E(erN)=exp[λ(er-1)], 此时复合P-G分布退化成一般Poisson分布.
定义2 设λ>0, 0≤γ<1, 称随机过程{N(t)}为服从参数为λ和γ的复合P-G过程,如果满足
1)N(0)=0;
2)N(t)具有独立平稳增量;
3)对任意t≥0, N(t)服从参数为λ和γ的复合P-G分布,且
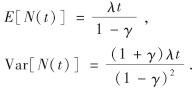
当γ=0时,复合P-G过程退化为一般的Poisson过程.
引理1[6] 设{N(t)}为服从参数为λ和γ的复合P-G过程,记α1=(λ(1-γ))/γ(若γ=0, 则取α1=λ),则当t足够小时,有
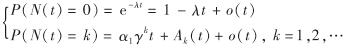
其中, Ak(t)=γk+(k-1)[γ(1+α1t)]k-2, 且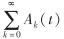 一致收敛.
一致收敛.
以下讨论假设保险赔付过程满足复合P-G过程的情况.
设u为初始盈余; S1(t)=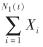 为保险公司截止时刻t的累积保费, Xi为第i次到达的保费额, N1(t)表示截止时刻t的投保发生次数,满足参数为λ1的Poisson过程; S2(t)=
为保险公司截止时刻t的累积保费, Xi为第i次到达的保费额, N1(t)表示截止时刻t的投保发生次数,满足参数为λ1的Poisson过程; S2(t)=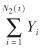 为保险公司截止时刻t的累积赔付, Yi为第i次索赔到来时的赔付额, N2(t)表示保险公司截止时刻t的赔付发生次数,满足参数为λ2和γ的复合P-G过程.保险公司根据初始盈余和单位时间内对赔付额度的预测来确定投资于风险资产的额度,文章假设其始终为F, 风险资产价格P(t)满足
为保险公司截止时刻t的累积赔付, Yi为第i次索赔到来时的赔付额, N2(t)表示保险公司截止时刻t的赔付发生次数,满足参数为λ2和γ的复合P-G过程.保险公司根据初始盈余和单位时间内对赔付额度的预测来确定投资于风险资产的额度,文章假设其始终为F, 风险资产价格P(t)满足
dP(t)=P(t)(μdt+σd(W(t)))
其中, μ为单位风险资产的收益率; σ为单位风险资产的波动率.同时,保险公司选择将剩余盈余全部投资到无风险资产.为了方便推导,假设无风险利率为0.因此,保险公司的盈余过程为
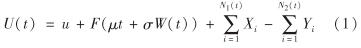
其中, W(t)为一维标准布朗运动; N1(t)、 N2(t)、 Xi、 Yi及W(t)相互独立.
保险公司考虑以b>0为界进行障碍分红,即当U(t)≥b时,保险公司将超过b的部分全部进行分红.称 为修正盈余,其中, D(t)为截止时刻t的累积分红.记τ=inf(t≥0:
为修正盈余,其中, D(t)为截止时刻t的累积分红.记τ=inf(t≥0: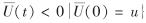 为破产时刻,定义Du,b(t)=
为破产时刻,定义Du,b(t)=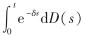 为时刻t的总红利现值.其中, δ≥0为折现因子; 0≤t≤τ.
为时刻t的总红利现值.其中, δ≥0为折现因子; 0≤t≤τ.
定义3 设ω(.,.)是一个二元非负可测函数,通常称为惩罚函数.又称
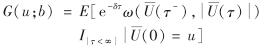
为破产时刻τ的期望折现罚金函数,也称Gerber-Shiu函数.其中,δ≥0为折现因子; 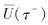 为破产前瞬间盈余;
为破产前瞬间盈余; 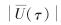 为破产时赤字; I为示性函数.一般地,假设G(u; b)关于u可微.
为破产时赤字; I为示性函数.一般地,假设G(u; b)关于u可微.
若ω(x,y)=1, 则当δ≠0时, ψ(u; b)=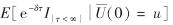 是保险公司破产时刻的Laplace 变换.
是保险公司破产时刻的Laplace 变换.
为方便证明,做如下假设.
假设保费额Xi服从参数为α的指数分布,记其分布函数为G1(x)=1-e-αx, 概率密度函数为g1(x). 索赔额Yj服从参数为β的指数分布,则可证 服从参数为(k, β)的Gamma分布,其概率密度函数
服从参数为(k, β)的Gamma分布,其概率密度函数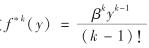 , 记
, 记
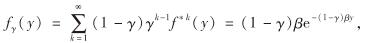
这表明累积赔付额服从参数为(1-γ)β的指数分布.在足够小的时间dt内,讨论保费和赔付的几种概率如下.
1)保费到来和赔付到来均为0次的概率.
P(N1(dt)=0, N2(dt)=0)=
[1-λ1dt+o(dt)][1-λ2dt+o(dt)]=
1-(λ1+λ2)dt+o(dt)
2)保费到来为0次,而赔付到来为k次的概率.
P(N1(dt)=0, N2(dt)=k)=
[1-λ1dt+o(dt)][α1γkdt+Ak(dt)+o(dt)]=
α1γkdt+Ak(dt)+o(dt)
3)保费到来1次,而赔付到来为0次的概率.
P(N1(dt)=1, N2(dt)=0)=
λ1dt[1-λ2dt+o(dt)]=λ1dt+o(dt)
4)其他情形下,事件发生的概率均为 o(dt).
定理1 当0≤u≤b时,Gerber-Shiu函数G(u; b)满足
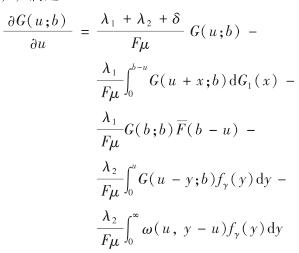
【证】当0≤u≤b时,在足够小的时间区间dt内,由盈余的马氏性及全期望公式有
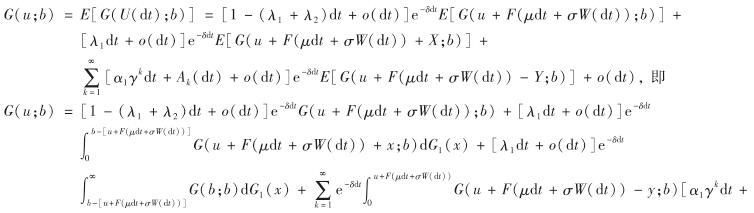
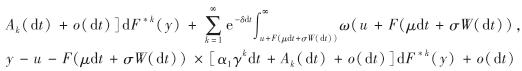
由引理1可知, 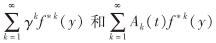 均一致收敛.再由单调收敛定理可知,积分与求和运算可以交换次序,同时不难推导
均一致收敛.再由单调收敛定理可知,积分与求和运算可以交换次序,同时不难推导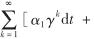
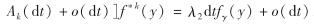 , 其中,
, 其中, 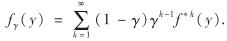 . 因此,
. 因此,
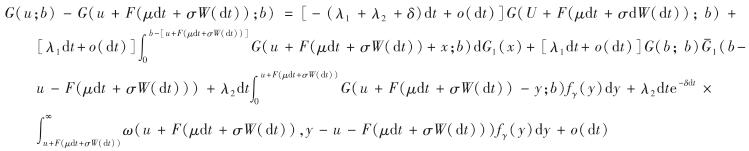
利用文献[13]的性质1及文献[8]中的无穷小方法,将上式两端同除以F(μdt+σdW(t)),并令dt→0, 则以概率1有积分-微分方程
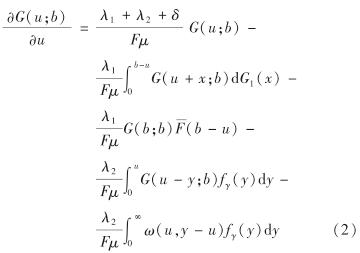
成立,并且当u≥b时,由于存在障碍分红,Gerber-Shiu函数满足G(u; b)=G(b; b),证毕.
结合定义3,由式(2)可知,在障碍分红下,破产时刻的Laplace变换ψ(u; b)满足

定理2 当0≤u≤b时,破产时刻的Laplace变换满足ψ(u; b)线性微分方程
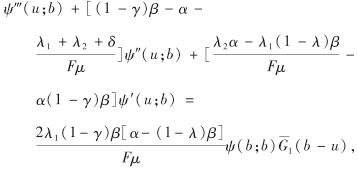
且满足ψ(u; ∞)=φ(u).
【证】为方便证明,首先做以下几个辅助工作.
在式(3)中,先换元,再对u求导,有

同时,若记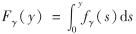 对u求导,有
对u求导,有
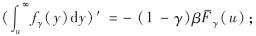
还有
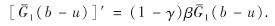
运用以上结果,推导定理结论.对式(3)两边关于u求导,有
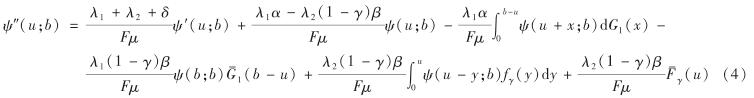
对式(4)两边关于u求导,有
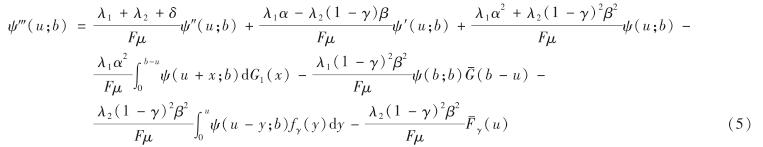
将式(3)乘以-α后与式(4)相加,有
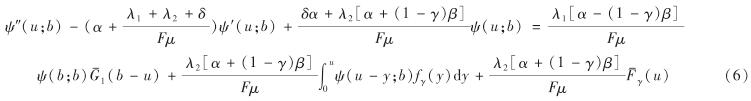
将式(4)乘以-α后与式(5)相加,有
ψ(u; b)-(α+(λ1+λ2+δ)/(Fμ))ψ″(u; b)+(λ2[α+(1-γ)β]+δα)/(Fμ)ψ'(u; b)-
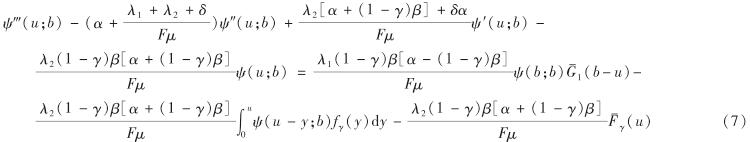
将式(6)乘以(1-γ)β后与式(7)相加,有
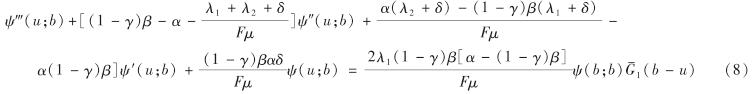
若记无分红时保险公司破产时刻的Laplace变换为φ(u), 则ψ(u; ∞)=φ(u), 且边界条件为
φ(∞)=0(9)
在式(8)中,若令b→∞, 则得到无分红情形下,破产时刻的Laplace变换φ(u)满足

定理3 无分红时保险公司破产时刻的Laplace变换为
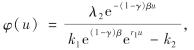
其中,
k1=(λ2(1-γ)β)/(r1+(1-γ)β);
k2=Fμr1-(λ1+λ2+δ)-
(λ1α)/(r1-α)+(λ2(1-γ)β)/(r1+(1-γ)β).
r1是特征方程(11)的唯一负根.
r3+[(1-γ)β-α(λ1+λ2)/(Fμ)]r2+
[(λ2α-λ1(1-γ)β)/(Fμ)-α(1-γ)β]r+
((1-γ)βαδ)/(Fμ)=0(11)
【证】方程(11)为方程(10)的特征方程.受文献[4]启发,不妨设方程(11)有3个不同的实根r1、 r2及r3, 则方程(10)的通解为
φ(u)=C1e<sup>r1u+C2e<sup>r2u+C3e<sup>r3u,
其中, C1、 C2及C3为任意常数.不难发现((1-γ)βαδ)/(Fμ)>0, 同时由于单笔赔付的期望1/((1-γ)β)会大于单笔保费的期望1/α, 进而(1-γ)β-α(λ1+λ2)/(Fμ)<0, 所以方程(11)的3个根之间必有r1<0<r2<r3. 注意到边界条件(9),于是必有C2=C3=0. 因此,方程(10)的通解为
φ(u)=C1e<sup>r1u(12)
以下求解C1. 若令b→∞, 则式(3)转化为
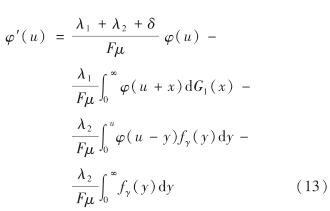
将式(12)代入式(13)得

从式(14)中可解出C1, 再将C1代入式(12),有
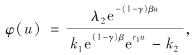
其中,
k1=(λ2(1-γ)β)/(r1+(1-γ)β);
k2=Fμr1-(λ1+λ2+δ)-
(λ1α)/(r1-α)+(λ2(1-γ)β)/(r1+(1-γ)β).
定理4 障碍分红下保险公司破产时刻的Laplace变换为
ψ(u; b)=φ(u)+A/(1-A)φ(b)e-α(b-u).
其中, A=-2((1-γ)β[α-(1-γ)β])/(α[α+(1-γ)β]).
【证】由于G -(b-u)=e-αbeαu, 显然α不是方程(11)的特征根,因此,不妨设Peαu为方程(8)的一个特解,进而
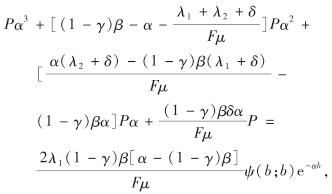
从中解得P=Aψ(b; b)e-αb, 其中,
A=-(2(1-γ)β[α-(1-γ)β])/(α[α+(1-γ)β]).
因此,方程(8)的通解为
ψ(u; b)=φ(u)+Aψ(b; b)e-αbeαu(15)
由式(15)可知ψ(b; b)=φ(b)+Aψ(b; b), 从中解出ψ(b; b), 并代入式(15),可得
ψ(u; b)=φ(u)+A/(1-A)φ(b)e-α(b-u).
结 语
在复合P-G风险下,本研究克服了仅单方面研究破产时刻的Laplace变换问题,或仅单方面研究带投资分红问题的局限,将带投资的障碍分红问题与破产时刻的Laplace变换问题统一起来,进行进一步研究.运用随机分析基本理论,得到带投资和障碍分红的破产时刻Laplac变换所满足的更新方程,并在指数分布假设下,得到复合P-G风险下投资和障碍分红破产时刻的Laplac变换显式解.
深圳大学学报理工版
JOURNAL OF SHENZHEN UNIVERSITY SCIENCE AND ENGINEERING
(1984年创刊 双月刊)
主 管 深圳大学
主 办 深圳大学
编辑出版 深圳大学学报理工版编辑部
主 编 李清泉
国内发行 深圳市邮电局
国外发行 中国国际图书贸易集团有限公司(北京399信箱)
地 址 北京东黄城根北街16号
邮 编 100717
电 话 0755-26732266
0755-26538306
Email journal@szu.edu.cn
标准刊号 ISSN 1000-2618
CN 44-1401/N